티스토리 뷰
INTRO
1. 상관 분석(Correlation Analysis)
- 피어슨 상관계수(Pearson Correlation Coefficient, PCC)
- 스피어만 상관계수(Spearman's Rank Correlation Coefficient, SRCC)
2. 다차원 척도법(Multi-Dimensional Scailing, MDS)
3. 주성분 분석(Principal Component Analysis, PCA)
3. 주성분 분석
상관관계가 있는 고차원 자료를 자료의 변동을 최대한 보존하는 저차원 자료로 변환시키는 방법으로 자료의 차원을 축약시키는데 주로 사용한다.
n차원 변수 $X = (X_1,X_2,...,X_n)^T$
첫번째 주성분 : $X$의 선형변환 $a_1^T$에서 $||a||=1$이고 분산이 가장 큰 선형변환 $Y_1 = a_1^T$
두번째 주성분 : $X$의 선형변환 $a_2^T$에서 $||a||=1$이고 첫번째 주성분과 상관계수가 0이면서 분산이 가장 큰 선형변환 $Y_2 = a_2^T$을 두번째 주성분이라 한다.
같은 방식으로 $Y_n = a_n^T$을 $n$번째 주성분까지 정의할 수 있다.
정의에 따라 주성분들은 서로 상관관계가 없고, 주성분들의 분산의 합은 $X_i$들의 분산의 합과 같다. $a_i$를 $i$번째 주성분의 로딩(loading)이라고 한다.
주성분들은 차원을 줄여 예측모델을 만들 때도 사용한다. 하래 그림과 같이 희생되는 정보가 가장 적은 방향을 결정한다.
[예제] PC data : 가격, 소프트웨어, 외형, 브랜드 만족도
test_PCA_1.R
rm(list=ls())
pc_data = read.csv("~/Rcoding/pc_data.csv")
pc_data_sub = subset(pc_data, select=c(Price, Software, Aesthetics, Brand))
pc_data_sub
pca <- princomp(~ ., data=pc_data_sub, cor=T)
# pca <- princomp(na.omit(pc_data_sub), cor=T)
pca_model = summary(pca,loadings=T)
pca_model
biplot(pca)출력결과
> rm(list=ls())
> pc_data = read.csv("~/Rcoding/pc_data.csv")
> pc_data_sub = subset(pc_data, select=c(Price, Software, Aesthetics, Brand))
> pc_data_sub
Price Software Aesthetics Brand
1 6 5 3 4
2 7 3 2 2
3 6 4 4 5
4 5 7 1 3
5 7 7 5 5
6 6 4 2 3
7 5 7 2 1
8 6 5 4 4
9 3 5 6 7
10 1 3 7 5
11 2 6 6 7
12 5 7 7 6
13 2 4 5 6
14 3 5 6 5
15 1 6 5 5
16 2 3 7 7
> pca <- princomp(~ ., data=pc_data_sub, cor=T)
> # pca <- princomp(na.omit(pc_data_sub), cor=T)
> pca_model = summary(pca,loadings=T)
> pca_model
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4
Standard deviation 1.5589391 0.9804092 0.6816673 0.37925777
Proportion of Variance 0.6075727 0.2403006 0.1161676 0.03595911
Cumulative Proportion 0.6075727 0.8478733 0.9640409 1.00000000
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4
Price 0.523 0.848
Software 0.177 0.977 -0.120
Aesthetics -0.597 0.134 0.295 0.734
Brand -0.583 0.167 0.423 -0.674
> biplot(pca)
summary 분석
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4 <-- 주성분 1,2,3,4
Standard deviation 1.5589391 0.9804092 0.6816673 0.37925777 <-- SD
Proportion of Variance 0.6075727 0.2403006 0.1161676 0.03595911 <-- 분산의 비율
Cumulative Proportion 0.6075727 0.8478733 0.9640409 1.00000000 <-- 누적비율
Comp.1이 60%, Comp.2까지 84.78%를 설명한다.
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4
Price 0.523 0.848
Software 0.177 0.977 -0.120
Aesthetics -0.597 0.134 0.295 0.734
Brand -0.583 0.167 0.423 -0.674
Comp.1는 높은 Price가 높을 수록 Aesthetics, Brand가 낮을 수록 높은 값을 가지고 Software의 영향은 적게 받는다.
Comp.2는 Software의 영향만 크게 받는다.
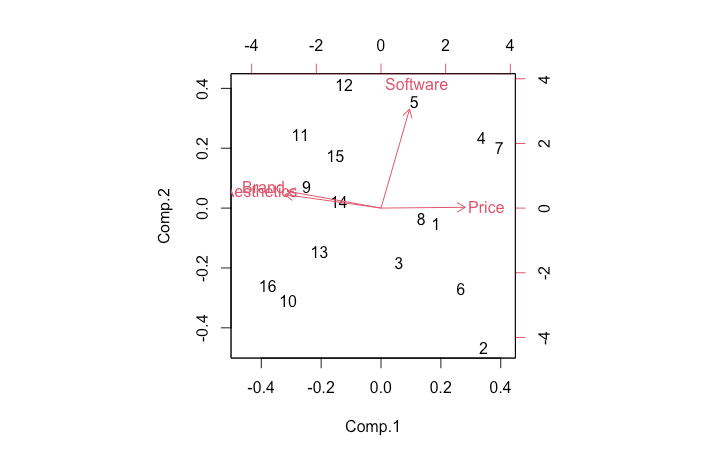
# Biplot은 첫번째 주성분(X축, 행), 두번째 주성분(Y축, 열) 값을 나타내는 행렬도를 시각화한 것
[예제] Noodle data : noodle, bowl, soup
주성분 분석(Principal Component Analysis, PCA) 두가지 방법 소개
princomp() : 상관계수행렬 또는 공분산행렬에 대한 Eigen Value Decomposition(EVD, 고유근분해)을 이용하여 계산한다.
prcomp() : 원 데이터에 대해 Singular Value Decomposition(SVD, 특이값분해)를 수행하여 계산한다.
test_PCA_2.R
rm(list=ls())
noodle_data = read.csv("~/R_coding/noodle_data.csv")
noodle_data_sub = subset(noodle_data, select=c(noodle,bowl,soup))
noodle_data_sub
## princomp
pca_evd = princomp(~ ., data=noodle_data_sub, cor=T)
pca_evd
pca_evd_model = summary(pca_evd,loadings=T)
pca_evd_model
biplot(pca_evd)출력결과
...
> ## princomp
> pca_evd = princomp(~ ., data=noodle_data_sub, cor=T)
> pca_evd
Call:
princomp(formula = ~., data = noodle_data_sub, cor = T)
Standard deviations:
Comp.1 Comp.2 Comp.3
1.2541347 0.9022241 0.7830312
3 variables and 10 observations.
> pca_evd_model = summary(pca_evd,loadings=T)
> pca_evd_model
Importance of components:
Comp.1 Comp.2 Comp.3
Standard deviation 1.2541347 0.9022241 0.7830312
Proportion of Variance 0.5242846 0.2713361 0.2043793
Cumulative Proportion 0.5242846 0.7956207 1.0000000
Loadings:
Comp.1 Comp.2 Comp.3
noodle 0.572 0.604 0.555
bowl 0.522 -0.790 0.322
soup 0.633 0.106 -0.767
> biplot(pca_evd)
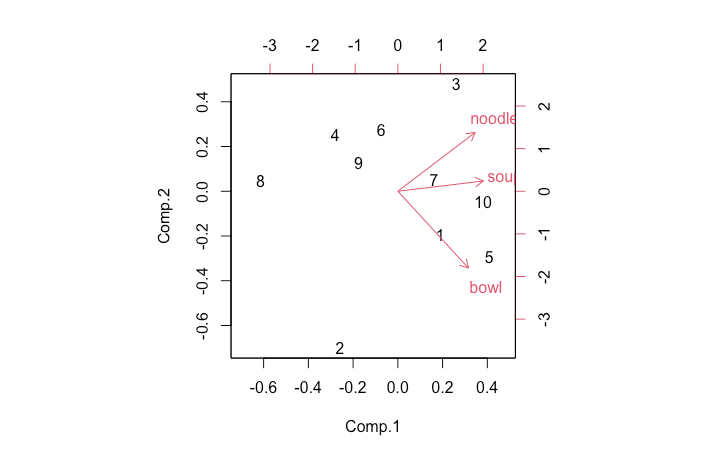
test_PCA_2.R
...
## prcomp
pca_svd = prcomp(noodle_data_sub, scale=T)
pca_svd
pca_svd_model = summary(pca_svd)
pca_svd_model
round(predict(pca_svd),2)
biplot(pca_svd)출력결과
...
> pca_svd = prcomp(noodle_data_sub, scale=T)
> pca_svd
Standard deviations (1, .., p=3):
[1] 1.2541347 0.9022241 0.7830312
Rotation (n x k) = (3 x 3):
PC1 PC2 PC3
noodle 0.5715110 -0.6044710 0.5549685
bowl 0.5221161 0.7896069 0.3223595
soup 0.6330639 -0.1055260 -0.7668731
> pca_svd_model = summary(pca_svd)
> pca_svd_model
Importance of components:
PC1 PC2 PC3
Standard deviation 1.2541 0.9022 0.7830
Proportion of Variance 0.5243 0.2713 0.2044
Cumulative Proportion 0.5243 0.7956 1.0000
> round(predict(pca_svd),2)
PC1 PC2 PC3
1 0.71 0.52 -1.37
2 -0.97 1.89 0.65
3 0.98 -1.29 0.00
4 -1.05 -0.68 -0.86
5 1.54 0.79 -0.73
6 -0.28 -0.74 0.68
7 0.60 -0.14 0.43
8 -2.31 -0.13 -0.18
9 -0.66 -0.34 0.31
10 1.43 0.12 1.08
> biplot(pca_svd)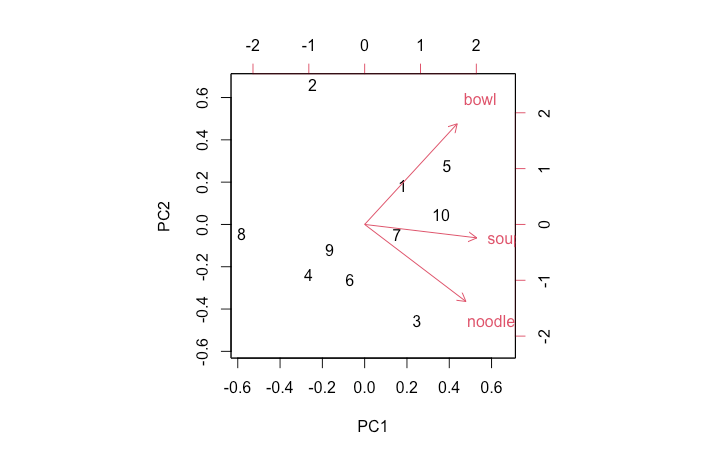
'R' 카테고리의 다른 글
| (macOS)[R] 시계열 예측 : 실습 - 1 (0) | 2022.04.18 |
|---|---|
| (macOS)[R] 시계열 예측 : 이론 (0) | 2022.04.18 |
| (macOS)[R] 다변량 분석 : 상관 분석(Correlation Analysis) - 3 (0) | 2022.04.16 |
| (macOS)[R] 다변량 분석 : 상관 분석(Correlation Analysis) - 2 (0) | 2022.04.16 |
| (macOS)[R] 다변량 분석 : 상관 분석(Correlation Analysis) - 1 (0) | 2022.04.16 |
- Total
- Today
- Yesterday
- arduino
- COVID-19
- ERP
- Pandas
- pyserial
- sublime text
- Regression
- 자가격리
- r
- Model
- template
- 코로나
- MacOS
- Raspberry Pi
- github
- analysis
- raspberrypi
- vscode
- Django
- DS18B20
- server
- 라즈베리파이
- 확진
- DAQ
- Templates
- git
- Python
- SSH
- CSV
- 코로나19
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
