티스토리 뷰
INTRO
1. 회귀분석이란?
2. 단순회귀분석
3. 다중회귀분석(중회귀분석)
4. 다항회귀분석
회귀분석 방법 : summary
- Residuals(잔차)
- Coefficients(회귀계수)
- 모델 적합도 : Multiple R-squared, Adjusted R-squared, F-statistic, p-value
다중회귀분석(Multiple Regression Analysis)
test_regression_2.R
rm(list=ls())
setwd = "~/Rcoding"
## multiple linear regression
set.seed(2)
u = runif(10,0,11)
v= runif(10,11,20)
w = runif(10,1,30)
y = 3 + 0.1*u + 3*v -3*w + rnorm(10,0,0.1)
dfrm = data.frame(y,u,v,w)
dfrm
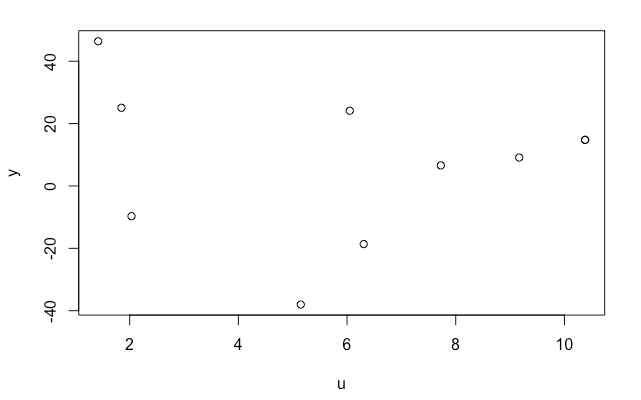
# plot-1, y vs. each u,v,w
plot(y ~ ., data=dfrm)출력결과
> source("~/R_coding/test_regression_2.R", echo=TRUE)
> rm(list=ls())
> setwd = "~/Rcoding"
> ## multiple linear regression
> set.seed(2)
> u = runif(10,0,11)
> v= runif(10,11,20)
> w = runif(10,1,30)
> y = 3 + 0.1*u + 3*v -3*w + rnorm(10,0,0.1)
> dfrm = data.frame(y,u,v,w)
> dfrm
y u v w
1 -9.690729 2.033705 15.97407 20.195064
2 6.593820 7.726114 13.15005 12.238937
3 -18.641259 6.306590 17.84462 25.269786
4 25.074657 1.848571 12.62738 5.364542
5 14.811383 10.382233 14.64754 11.070895
6 14.769441 10.378225 18.68194 15.174424
7 46.400364 1.420749 19.78759 5.328159
8 9.108600 9.167937 13.03243 11.354815
9 -38.029897 5.148204 15.00328 28.916677
10 24.113556 6.049821 11.67481 4.838788
> # plot-1, y vs. each u,v,w
> plot(y ~ ., data=dfrm)
Hit <Return> to see next plot:
독립변수 u, v, w 에 따른 종속변수 y의 분포
선형 회귀 모델 진단 그래프(Linear Regression Model Diagnostic Graph)
test_regression_2.R
...(이상 동일)....
# plot-2, OLS(Ordinary Least Squares) model diagnostic
model = lm(y ~ u+v+w, data=dfrm)
model
summary(model)
plot(model)
## 2,2 subplot type
# par(mfrow=c(2,2))
# plot(model)출력결과
...(중략)...
> # plot-2, OLS(Ordinary Least Squares) model diagnostic
> model = lm(y ~ u+v+w, data=dfrm)
> model
Call:
lm(formula = y ~ u + v + w, data = dfrm)
Coefficients:
(Intercept) u v w
3.0417 0.1232 2.9890 -2.9978
> summary(model)
Call:
lm(formula = y ~ u + v + w, data = dfrm)
Residuals:
Min 1Q Median 3Q Max
-0.188562 -0.058632 -0.002013 0.080024 0.143757
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.041653 0.264808 11.486 2.62e-05 ***
u 0.123173 0.012841 9.592 7.34e-05 ***
v 2.989017 0.016586 180.215 1.97e-12 ***
w -2.997816 0.005421 -552.981 2.36e-15 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1303 on 6 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 1
F-statistic: 1.033e+05 on 3 and 6 DF, p-value: 1.588e-14
> plot(model)
Hit <Return> to see next plot:
Hit <Return> to see next plot:
Coefficients:
(Intercept), u, v, w 모두 *** p-value < 0.001을 만족한다.
Multiple R-squared = Adjusted R-squared = 1로 회귀식이 데이터를 매우 잘 설명한다.
따라서 하나의 종속변수 y는 다중 독립변수 u,v,w 간에 선형관계를 가진다고 추정할 수 있으며 회귀식은 다음과 같다.
$ y = 3.0417 + 0.1232*u + 2.9890*v -2.9978*w $
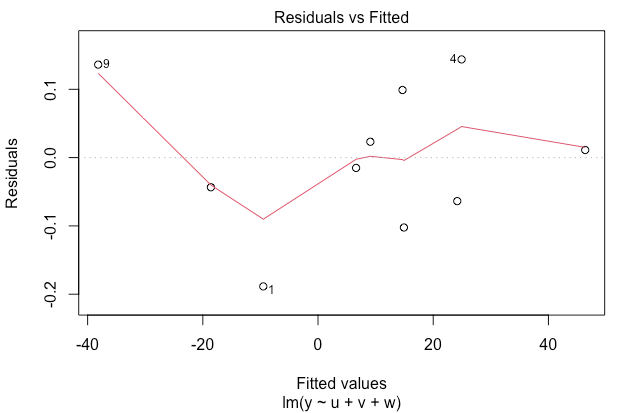
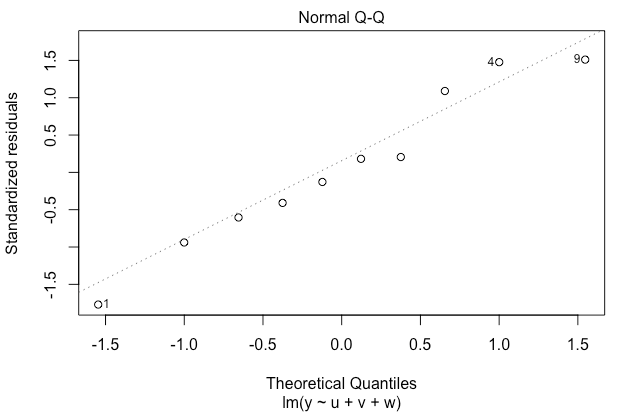
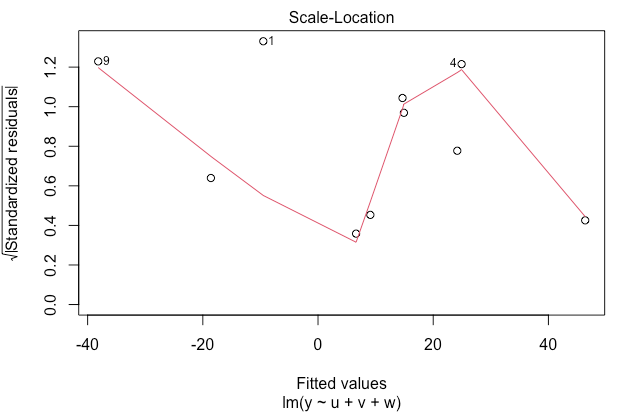

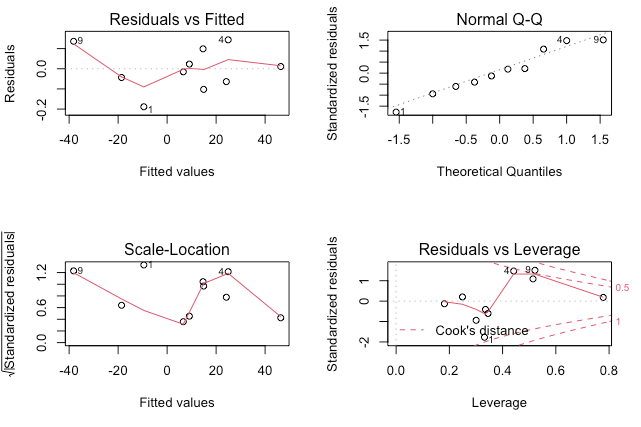
Fig.1: Residuals vs Fitted
- 정규성(Normality) 확인
- 선형 회귀에서 오차는 평균이 0이고 분산이 일정한 정규 분포를 가정
- 예측된 y 값과 무관하게 잔차의 평균은 0이고 분산은 일정해야 한다.
- 따라서 이 그래프에서는 기울기 0인 직선이 관측되는 것이 이상적이다.
- u,v,w 다중 독립변수에 의한 선형 회귀로 예측된 y의 잔차인 Residuals가 0에 가깝게 분포한다.
Fig.2 : Normal Q-Q
- 정규성(Normality) 확인
- 표준화된 잔차(Standardized Residuals)의 확률(Probability) plot
- 잔차가 정규 분포를 따르는지 확인하기 위한 chart
- 각 점들이 기울기가 1인 직선에 가까울수록 정규성 가정을 만족한다.
Fig.3 : Scale-Location
- 등분산성(Homoscedasticity) 설명
- 선형 회귀로 예측된 독립변수를 Y 축에 표준화 잔차 절대값의 제곱근
- 이 경우도 기울기가 0인 직선이 이상적이다.
- Y축 0에서 멀리 떨어진 값이 관찰된다면 해당 점은 회귀 직선에 적합하지 않으며 이상치(outlier)일 가능성이 있다.
Fig4. Residuals vs Leverage
- X축 Leverage, Y축 표준화된 잔차(Standardized Residuals)
- Leverage는 독립변수(설명변수)가 얼마나 극단에 치우쳐 있는지를 나타내며 outlier, high leverage point, influential observation로 구분한다.
outlier : 회귀 모형으로 잘 예측되지 않는 관측치
high leverage point : 예측 변수의 이상치(outlier)
influential observation : 통계 모형 계수 결정에 불균형한 영향을 미치는 관측치, Cook's distance 통계치로 확인.
반응형
'R' 카테고리의 다른 글
| (macOS)[R] 기초 통계 분석 : 최적 회귀 방정식 선택(설명변수 선택) - 1 (0) | 2022.04.14 |
|---|---|
| (macOS)[R] 기초 통계 분석 : 회귀 분석(Regression Analysis) - 4 (0) | 2022.04.13 |
| (macOS)[R] 기초 통계 분석 : 회귀 분석(Regression Analysis) - 2 (0) | 2022.04.07 |
| (macOS)[R] 기초 통계 분석 : 회귀 분석(Regression Analysis) - 1 (0) | 2022.04.05 |
| (macOS)[R] 기초 통계 분석 : 기술 통계 (0) | 2022.04.05 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- SSH
- github
- template
- Model
- Regression
- DS18B20
- 코로나
- 확진
- Python
- ERP
- arduino
- DAQ
- Raspberry Pi
- sublime text
- MacOS
- r
- COVID-19
- git
- server
- Pandas
- vscode
- Django
- pyserial
- analysis
- 코로나19
- 자가격리
- 라즈베리파이
- Templates
- raspberrypi
- CSV
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
글 보관함
